A statistical filter for state likelihood estimation: the Kalman filter.
Introduction
The Kalman filter : Overview, Algorithm, Example: Sensor fusion, Example: Vehicle entering a tunnel
Other features : Control signal input, Error estimation, Time-variant covariance matrices, Further notes
List of ini keys
This filter suite implements a particle and a Kalman Filter.
Disclaimer: The Kalman and particle filters are not meant for operational use, rather they aim to be an accessible framework to scientific research backed by the convenience of MeteoIO, to quickly try a few things.
What do they do?
Both filters follow a statistical approach. The particle filter is a classical Monte Carlo method and samples states from a distribution function. The Kalman filter solves matrix equations of Bayesian statistics theory. They solve the problem of combining model data with noisy measurements in an optimal way.
Who are they for?
a) Suppose you have your toolchain set up with MeteoIO and are interested in Bayesian filters. With this software, you can (relatively) easily start to explore in this direction and hopefully decide if it is an idea worth pursuing.
b) You try a filter, play with the settings, and for whatever reason it works.
The difference to other, easier to use, filters is that you, the user, must provide the Physics in form of analytical models and covariance matrices. Almost all will be defaulted, but this may not make much sense in your use case.
A Kalman filter works on a linear state model which propagates an initial state forward in time. At each time step, the filter will adjust this model taking into account incoming measurements tainted with white (Gaussian) noise. For this, we can tune how much trust we put in our measurements (initial and online), and thus how strongly the filter will react to observations.
You need your linear model function in matrix form, initial values at \(T=0\) and a second model that relates observations to the internal states. If the model describes the measured parameters directly, this is the identity matrix. You supply an initial trust in the initial states, and this matrix will be propagated as error estimation. Furthermore, you assign a level of trust in the model function, and a level of trust in the measurements.
The Kalman filter solves the following set of recursive equations:
Prediction:
\[ \hat{x}_k=A\hat{x}_{k-1} + B u_k \]
\[ P_k = A P_{k-1}A^T+Q \]
Update:
\[ K_k = P_k H^T(H P_k H^T + R)^{-1} \]
\[ \hat{x}_k = \hat{x}_k + K_k(\hat{z}_k - H\hat{x}_k) \]
\[ P_k = (I - K_k H)P_k \]
where \(\hat{x}_k\) is the model value at time step \(k\), \(A\) is the model itself, i. e. the system transformation matrix, \(u_k\) is a control signal that is related to the states via \(B\), \(P\) is an error estimation, and \(Q\) is the covariance matrix of the process noise. Furthermore, \(\hat{z}_k\) is the observation at time step \(k\), \(K\) denotes the Kalman gain, \(H\) is the observation model relating observations to the states, \(R\) is the observation covariance matrix, and \(I\) is the identity. For details see Ref. [AM+02] equations (8)-(16).
Let's start with a real-world example and work through the settings.
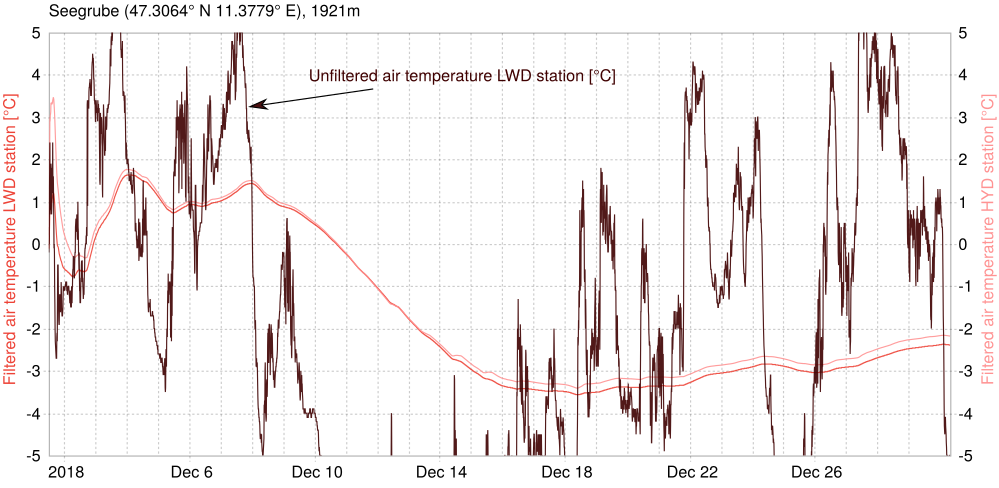
/doc/examples/statistical_filters.cc program to follow along.At Innsbruck's Seegrube, there is a spot were two stations from different owners are situated right next to each other. Of course they both measure the air temperature and we want to use the Kalman filter to find the most likely real temperature.
First, we need the heart of the problem, our system model. It describes the evolution of the states through time and is read from the STATE_DYNAMICS key. This is the matrix A from above. Matrices can be input in three different ways:
1, 0, 0, 1. You can put brackets around your numbers for readability: [1, 0][0, 1].We will use a most easy model:
This means that we assume a constant temperature throughout our data window.
Next, we need an initial state. We have two internal states (both of which are energy states), namely the two temperatures. For both filters, you can provide the values as a list (e. g. 268, 271). You can also leave all of them or some of them empty to make MeteoIO pick the initial state(s) from the 1st available observation(s). "1st" is a synonym for this. You can use the token "average" (case sensitive) to let MeteoIO average over all 1st observations. We want the average between the first measurement of both stations so we write:
[268, ] (to set the first state to 268 and pick the earliest measurement of the second observation variable for the 2nd state. Identical: [268, 1st]). We have our states initialized and our state transition matrix ready. Now we need some statistical quantities. We provide the trust in the initial state via the INITIAL_TRUST key. This inputs the matrix P from above. Set low values if you don't trust \(\hat{x}_0\), and very high ones if you do. Let's not worry about it too much and pick a not very trusty 1 at the diagonal:
[1, 0] [0, 1] (full matrix), [1, 1] (diagonal vector), or 1, 1 (you do not need brackets).Next, we need the covariance of the process noise (noise in the model function by external forces acting on the state variables). A poor process model might be mitigated by injecting enough uncertainty here. We don't have knowledge of any specific process disturbances but we know that our model is quite crude, so we inject a bit of uncertainty in the model:
[0.05, 0][0, 0.05].We now have everything regarding the system model. On to the observations.
The matrix \(H\) from above is the observation model relating our measurements to the internal states. In our case, we measure the temperatures which are also our internal states, so there is nothing to do. We can however decide how much each station contributes to the estimate. Let's trust both stations the same:
Next, the matrix \(R\) which is the observation covariance. Let's assume a standard deviation sigma of 0.8, i. e. the uncertainty of the sensor is somewhere around 0.8 °C and we put the variance (sigma squared) on the diagonal:
Only thing missing is a list of parameters that stand for the states. The filter runs on TA which is the first state, and we want the second one to be TA_HYD. By default, MeteoIO will only filter TA in the output file. This is to comply with all other filters and avoid unexpected results. We can set however that all observations that are filtered internally are also filtered in the meteo set:
Note that we require the number of observables to be equal to the number of states, simply to avoid having to set how many, and which, observables to output. You must supply them, but you can easily discard them (e. g. by leaving FILTER_ALL_PARAMETERS = FALSE or by designing your matrices in a way that they zero out).
Important: For technical reasons, filtering other parameters than the one the filter runs on only works as expected when the Kalman filter is the last filter that is applied!
COPY command.The complete ini section now reads:

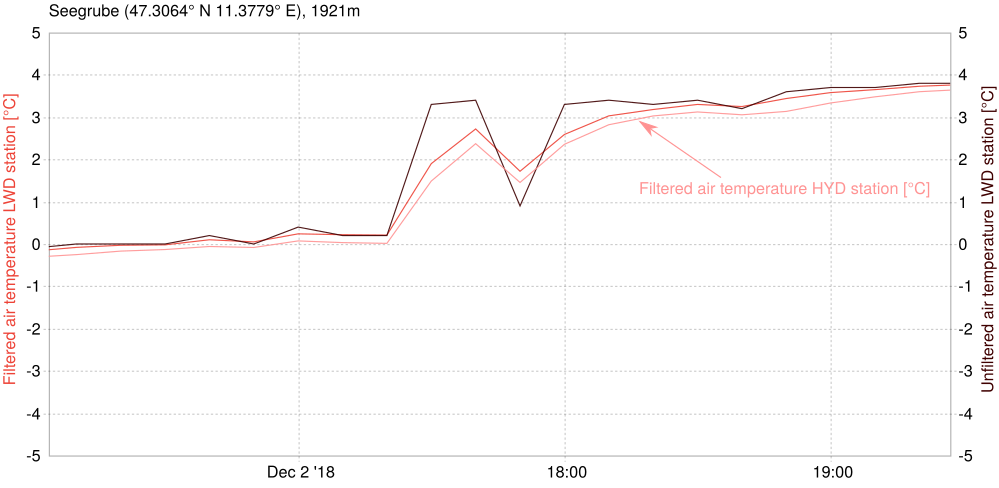
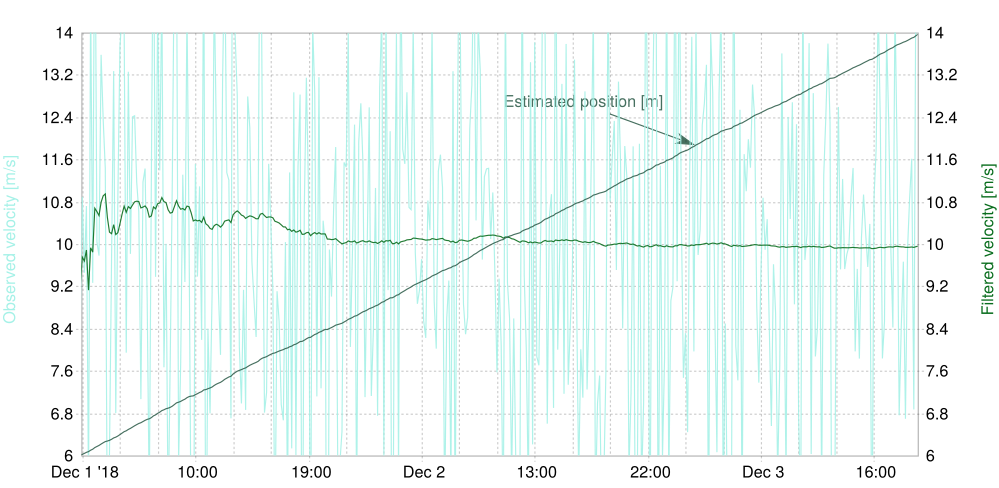
Let's tackle an accessible non-meteo standard problem for a Kalman filter to help understand the input mechanics better. Suppose a car enters a tunnel and can still reliably measure its speed, but not its position.
/doc/examples/statistical_filters.cc fakes noisy measurements of the velocity in x-direction (a constant true speed plus noise) and MeteoIO will read this in the SPEED parameter.This is our model for the position and (constant) speed:
\[ x_t = x_{t-1} + \frac{\mathrm{d}x_{t-1}}{\mathrm{d}t} * dt \]
\[ \frac{\mathrm{d}x_t}{\mathrm{d}t} = \frac{\mathrm{d}x_{t-1}}{\mathrm{d}t} \]
x-direction and \(v_y\) remains zero.We fix our state vector to be ordered [position in x, position in y, speed in x, speed in y]:
\[ \hat{x}=\left( \begin{array}{c} x \\ y \\ v_x \\ v_y \end{array} \right) \]
Therefore, the system model can be written in matrix form such that \(\hat{x}_t = A\hat{x}_{t-1}\):
\[ A=\left( \begin{array}{cccc} 1 & 0 & dt & 0 \\ 0 & 1 & 0 & dt \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \]
To select the measured velocities we design H to be:
\[ H=\left( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \]
Keep in mind that we are only measuring the velocities, not the positions, so only the velocities can play a role in the new state estimation (Eq. 2 of update step). The initial values are position \((0, 0)\) and speed \((x_0, 0)\), and we pick the first measured speed as initial value:
H could then be a 2x4-matrix, R could be a 2x2-matrix and the formulas would still work out. However, since all states are propagated anyway it is next to no penalty to work with square matrices and output them all.With our states ordered the way they are the filter must run on x so that this is also internally the first observable. Then we match the rest of our vector ordering:
With some covariances (we have a perfect model now) and error output the whole ini section reads like so:
With CONTROL_SIGNAL you can input an external control signal acting on the states (the vector \(\hat{u}\) from above) in three different ways:
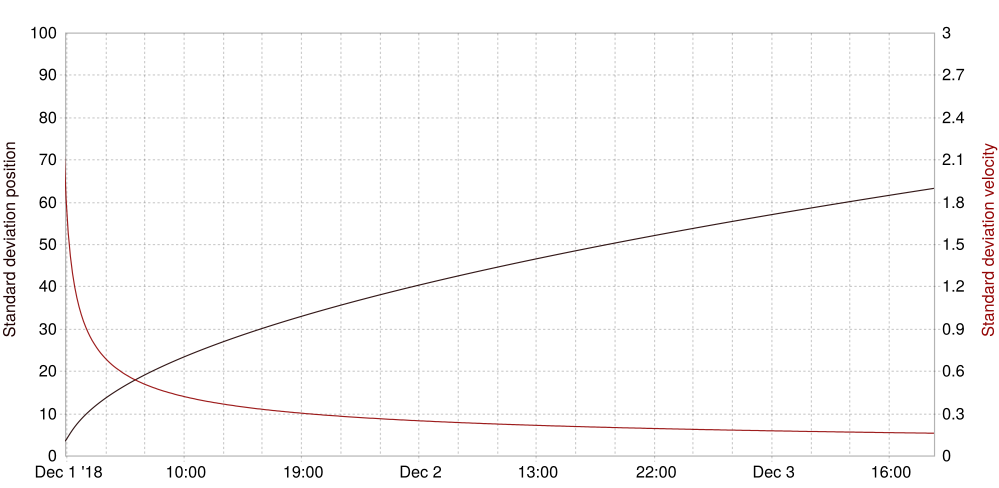
0.2) that an appropriate vector is filled with.[0.1, 0.2]) which will be applied for all time steps.UU1 UU2), i. e. a time-variant vector. The matrix \(H\) is applied to this vector and can be input via CONTROL_RELATION as usual.OUT_ESTIMATED_ERROR lets you pick one or more field names that the filter will output the evolution of the diagonal elements of the error estimation \(P\) to. Considering the diagonal elements to be variances you can also take the square root of this value for convenience with the OUT_ERROR_AS_STDDEV key.
If you have two states, you need two parameter names (that will be created).
With PROCESS_COVARIANCE_PARAMS and OBSERVATION_COVARIANCE_PARAMS you can supply a list of parameters that \(Q\) and \(R\) are read from, i. e. time-variant covariance matrices. This has priority over a fixed matrix that is found in PROCESS_COVARIANCE and OBSERVATION_COVARIANCE, respectively. They can only be input as vectors that will be put on a matrix diagonal with the rest being 0. For this you need one meteo parameter per vector element (state) and you need to name the parameters with PROCESS_COVARIANCE_PARAMS and OBSERVATION_COVARIANCE_PARAMS.
The VERBOSE keyword can be used to enable/disable some warnings the filter shows in the console. This will normally concern missing input that was defaulted or something similar. Usually you will want to get rid of all of them, but if the filter must be quiet no matter what then you can set VERBOSE = FALSE.
PROCESS_COVARIANCE_PARAMS = COV1 COV2 COV3).[DATASOURCEXXX] command to read multiple input files and stream them to the same container useful to combine meteo data and model input.BUFF_BEFORE and BUFFER_SIZE keys. If you set both to 0 then the filters receive exactly the time frame covered by the input dates. However, if you are using windowed filters also, then these will lack data. This is important in understanding how the initial states are picked: if MeteoIO inits the states automatically with the first available data point then this is taken from the first point MeteoIO sees. Thus, with a large enough buffer the model will start at a much earlier date and initial states are also picked a while before the input start date. Additionally, if there are nodata elements in there then even if they would be ignored for the output they would make the filters display warnings. You have to be careful to either start your analytical model at the date data window - buffer, or ideally provide exactly the same amount of data on the file system as you request MeteoIO to filter.| Keyword | Meaning | Optional | Default Value |
|---|---|---|---|
| STATE_DYNAMICS | State transition matrix ( \(A\)). | no | - |
| INITIAL_STATE | State of the system at T=0 ( \(\hat{x}_0\)). | yes | empty, meaning 1st measurement will be picked |
| INITIAL_TRUST | Trust in the initial state ( \(P_0\)). | yes | 1, meaning an appropriate identity matrix |
| PROCESS_COVARIANCE | Process noise covariance matrix (trust in the model, \(Q\)). | yes | 0, meaning a matrix with all zeros |
| ADD_OBSERVABLES | List of observables in addition to the one the filter runs on. | yes | empty, meaning we have 1 state resp. 1 observable |
| FILTER_ALL_PARAMETERS | Filter only the parameter the filter runs on, or all states? | yes | FALSE, but TRUE is useful |
| OBSERVATION_RELATION | Linear model relating the observations to the states ( \(H\)). | yes | 1, meaning identity matrix |
| OBSERVATION_COVARIANCE | Observation noise covariance matrix (trust in the measurements, \(R\)). | yes | 0 |
| CONTROL_SIGNAL | External control signal acting on the states ( \(\hat{u}\)). | yes | 0 |
| OUT_ESTIMATED_ERROR | Parameter name(s) to output error evolution to. | yes | empty |
| OUT_ERROR_AS_STDDEV | If TRUE, take the square root of error parameters. | yes | FALSE |
| PROCESS_COVARIANCE_PARAMS | List of parameter names to read \(Q\) from. | yes | empty |
| OBSERVATION_COVARIANCE_PARAMS | List of parameter names to read \(R\) from. | yes | empty |
| VERBOSE | Output warnings to the console. | yes | TRUE, warnings should be mitigated |
Read on at FilterParticle.
#include <FilterKalman.h>
Public Member Functions | |
| FilterKalman (const std::vector< std::pair< std::string, std::string > > &vecArgs, const std::string &name, const Config &cfg) | |
| virtual void | process (const unsigned int ¶m, const std::vector< MeteoData > &ivec, std::vector< MeteoData > &ovec) |
| The filtering routine as called by the processing toolchain. More... | |
 Public Member Functions inherited from mio::ProcessingBlock Public Member Functions inherited from mio::ProcessingBlock | |
| virtual | ~ProcessingBlock () |
| virtual void | process (Date &dateStart, Date &dateEnd) |
| std::string | getName () const |
| const ProcessingProperties & | getProperties () const |
| const std::string | toString () const |
| bool | skipStation (const std::string &station_id) const |
| Should the provided station be skipped in the processing? More... | |
| bool | noStationsRestrictions () const |
| const std::vector< DateRange > | getTimeRestrictions () const |
Additional Inherited Members | |
 Static Public Member Functions inherited from mio::ProcessingBlock Static Public Member Functions inherited from mio::ProcessingBlock | |
| static void | readCorrections (const std::string &filter, const std::string &filename, std::vector< double > &X, std::vector< double > &Y) |
| Read a data file structured as X Y value on each lines. More... | |
| static void | readCorrections (const std::string &filter, const std::string &filename, std::vector< double > &X, std::vector< double > &Y1, std::vector< double > &Y2) |
| Read a data file structured as X Y1 Y2 value on each lines. More... | |
| static std::vector< double > | readCorrections (const std::string &filter, const std::string &filename, const size_t &col_idx, const char &c_type, const double &init) |
| Read a correction file applicable to repeating time period. More... | |
| static std::vector< offset_spec > | readCorrections (const std::string &filter, const std::string &filename, const double &TZ, const size_t &col_idx=2) |
| Read a correction file, ie a file structured as timestamps followed by values on each lines. More... | |
| static std::map< std::string, std::vector< DateRange > > | readDates (const std::string &filter, const std::string &filename, const double &TZ) |
| Read a list of date ranges by stationIDs from a file. More... | |
 Protected Member Functions inherited from mio::ProcessingBlock Protected Member Functions inherited from mio::ProcessingBlock | |
| ProcessingBlock (const std::vector< std::pair< std::string, std::string > > &vecArgs, const std::string &name, const Config &cfg) | |
| protected constructor only to be called by children More... | |
 Static Protected Member Functions inherited from mio::ProcessingBlock Static Protected Member Functions inherited from mio::ProcessingBlock | |
| static void | extract_dbl_vector (const unsigned int ¶m, const std::vector< MeteoData > &ivec, std::vector< double > &ovec) |
| static void | extract_dbl_vector (const unsigned int ¶m, const std::vector< const MeteoData * > &ivec, std::vector< double > &ovec) |
 Protected Attributes inherited from mio::ProcessingBlock Protected Attributes inherited from mio::ProcessingBlock | |
| const std::set< std::string > | excluded_stations |
| const std::set< std::string > | kept_stations |
| const std::vector< DateRange > | time_restrictions |
| ProcessingProperties | properties |
| const std::string | block_name |
 Static Protected Attributes inherited from mio::ProcessingBlock Static Protected Attributes inherited from mio::ProcessingBlock | |
| static const double | soil_albedo = .23 |
| static const double | snow_albedo = .85 |
| static const double | snow_thresh = .1 |
| parametrize the albedo from HS More... | |
| mio::FilterKalman::FilterKalman | ( | const std::vector< std::pair< std::string, std::string > > & | vecArgs, |
| const std::string & | name, | ||
| const Config & | cfg | ||
| ) |
|
virtual |
The filtering routine as called by the processing toolchain.
| [in] | param | Parameter index the filter is asked to run on by the user. |
| [in] | ivec | Meteo data to filter. |
| [out] | ovec | Filtered meteo data. Cf. main documentation. |
Implements mio::ProcessingBlock.